Graphical Abstract

Abstract

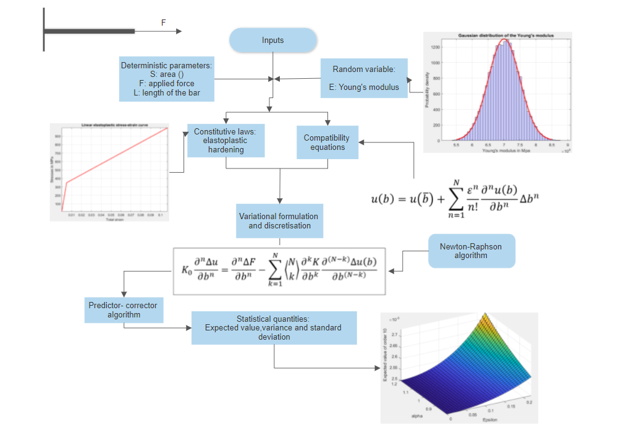
From skyscrapers to stealth fighters, passing through tiny electronic components embedded in electronic devices, engineering structures are in nature very sensitive to material uncertainties. Indeed, any small defect that usually occurs due to some known or unknown reasons during the production process of a structure’s components, can in some cases be very prejudicial or even endanger the usage or functionality expected from the structure in operation. Since conventional engineering designs usually rely on a fully deterministic analysis of the problem just by considering the mean values of observed random variables, it is worth it to integrate the perturbation caused by the dispersion of random variables around its mean and investigate its repercussions on the response of the structure. That being said, this paper treats especially the stochastic finite element analysis of both linear and nonlinear elastoplastic tensile bar problems with young’s modulus considered as a Gaussian random variable. To this end, the formulation adopted is based on the stochastic perturbation method where the expected value (stochastic displacement field) is expanded to the 10^th order on the Taylor expansion series with perturbation factor. In compliance with the general stochastic perturbation-based method, the problem is firstly treaded as deterministic where the displacement field and its first 10 derivatives are obtained successively (the predictor-implicit Backward-Euler Algorithm is employed for the incremental integration of elastoplastic models with isotropic and kinematic hardening). With the later quantities at hand, two-variable polynomial expressions of the expected value, variance and standard deviation are deduced in a straightforward manner. Finally, the study and visualisation of these statistical quantities are performed, and informative notes are drawn out after comparing with the deterministic value of the displacement. The algorithms developed here have been all implemented into MATLAB. The approach proposed here makes it possible to consistently take into account certain material property uncertainties without too much computational effort.

Keywords

Perturbation; elastoplastic; Gaussian; stochastic, predictor-corrector.

Acknowledgement

The authors acknowledge the funding provided by the  University of  Pardubice through research grant numbers SGS  2022 and SGS_202 2 _0 09  (DFJP  UPA).

References

1. Kamiński, M.; The Stochastic Perturbation Method for Computational Mechanics, 2013.
   DOI: 10.1002/9781118481844.
2. Öchsner, A.; Elasto-Plasticity of Frame Structure Elements, 2014. DOI: 10.1007/978-3-662-44225-8.
3. Borja, R. I.; Plasticity: Modeling & Computation, Vol. 4, no. 3. 2013. [Online]. Available: http://link.springer.com/10.1007/978-3-642-38547-6.

Biography

Sadjiep Tchuigwa B. S. prior to joining the University of Pardubice for his PhD studies started in early 2020, Sadjiep Tchuigwa Baurice Sylvain received a Bachelor’s degree and a Master’s degree in Civil Engineering from the Faculty of Industrial Engineering of the University of Douala (Cameroon) respectively in 2014 and 2016. Afterward, between 2016 and 2019, he had been working actively on both residential and industrial construction projects as Civil engineer and consultant in Cameroon and Gabon. His main research interests are concerned with structural engineering with a particular focus on Computational Mechanics and High-Performance computing. Under the supervision of Assoc. Prof. Jan Krmela, PhD, his current doctoral thesis deals with numerical simulation of car tires under dynamic loads.