Graphical Abstract

Abstract

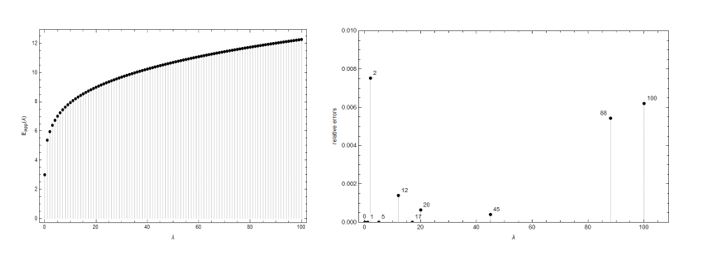
Approximate analytic solutions have been found for the excited states eigenvalues of the anharmonic potential x²+λx⁸. In a previous publication, analytic approximation functions were determined for the ground state eigenvalue of this potential [1]. However, the excited states are so important as the ground states. Thus, here the analysis of this potential has been extended by including analytic approximations for the first excited states with enough accuracy for most of the applications. Numerical calculations can be performed to determine the eigenvalues for a given value of λ, using for instance Borel-Pade method or Hill determinants [2], but the aim now is to determine and analytic function for each excited states good for any positive value of λ. The problems with the excited states are rather different to the case of ground state, but some general ideas are followed as those described in previous works [3]. Thus, the starting point is to find two expansions in λ for each excited state, one good for small values of λ, and the other for large values. Later an analytic function in λ has to be found, which will be as a bridge between both previous expansions. This function will be a combination of rational functions (quotient of two polynomials) and fractional powers. The way to determine the parameters of the approximations for the first excited states will be described in detail, as well as their accuracy. Two figures are including here corresponding to the results with second degree polynomials for the first excited state. The first figure is for the eigenvalues as a function of λ. The second figure is for the relative errors also as a function of λ. The maximum relative error is about 0.008, But most of the relative errors are much smaller than that value. The largest error are for small values of λ in a region around the point with the maximum error.

References

1. P. Martin, F. Maass and D. Diaz-Almeida, “Accurate analytic approximation to the eigenvalues of the anharmonic potential x²+λx⁸”, Results in Phys., 2020, 16, 102986 (4 pp.).
2. S.N. Biswas, K. Datta, R. P. Saxena, P. K. Srivastava and  V. S. Varma, “Eigenvalues of λx^2m anharmonics oscillators”, J. Math. Phys., 1973, 14, 1190.
3. P. Martin, E. Castro, J. L. Paz and A. DeFreitas, “Multipoint Quasirationals Approximants in Quantum Chemistry”, Chapter 3 of  “New Developments in Quantum Chemistry” by J. L. Paz and  Hernandez (Transworld Research Network, Kerala, India, 2009).

Biography

Pablo Martin was born in Madrid, Spain, on June 30,1937. He received the degree in Ingeniero Civil Industrial (Distinción Unánime) from the Universidad de Chile, Facultad de Ciencias Físicas y Matemáticas, Chile, in 1964. He was Assistant Professor in Rational Mechanics (Mecánica Racional) at the “Escuela de Ingeniería, Universidad de Chile” and later Catedrático until 1969. He got a scholarship from the Ford Foundation, and he received his MSc. of Sciences, and Ph.D. degree in Plasma Physics from the University of California, Los Angeles (UCLA), USA, in 1971. He was Subdirector Técnico and Director Ejecutivo Encargado in Comisión Chilena de Energía Nuclear, COCHEN, on 1972 and 1973. He has been Researcher and Professor at the Universidad Simon Bolivar in Caracas, Venezuela, and Universidad de Antofagasta, Chile, from 1974 until now. He has been Visiting Professor several times at the Imperial College (London,UK), UCLA ( U. California, USA) and U. Campinas (Estdo. Sao Paulo, Brasil). He has been Collaborator for one year in Los Alamos National Laboratory (T-11 group, directed by A. R. Bishop), USA. He has published or edited 4 books and published about 165 papers in International Journals on Plasma Physics, Biophysics, Quantum Physics, Geophysics and others fields of Physics and Engineering. He has been Vice-president of the Sociedad Venezolana de Física, SVF, for two years. He is Life Senior member of the IEEE, and member of the APS, SEG and OSA in USA and SOCHIFI in Chile. He is author of three different International Invention Patents, two of them in USA, as well as other countries.